Call:
lm(formula = IQ ~ SES, data = nlschools)
Residuals:
Min 1Q Median 3Q Max
-8.2659 -1.1651 0.0345 1.2147 6.4551
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.163000 0.112430 90.39 <2e-16 ***
SES 0.060084 0.003764 15.96 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.963 on 2285 degrees of freedom
Multiple R-squared: 0.1004, Adjusted R-squared: 0.09996
F-statistic: 254.9 on 1 and 2285 DF, p-value: < 2.2e-16MLM Seminar - Sitzung 4
Lineare Regression - Modellspezifikation und Modellparameter
Modelschätzung
Modelvorhersahen
# beta 0 (Intercept)
b0 = 10.163000
# beta 1 (Steigung)
b1 = 0.060084
# X-Werte für die erwartete Y-Werte geschätzt werden sollen
x = 0:10
# Schätzen wir die Y-Werte mit der Formel der Regression
vorhersagen <- b0 + b1 * x
# Speichern wir die Ergebnisse in einer Tabelle
vorhersagen_df <- data.frame(SES = x, IQ = round(vorhersagen, 3))Visualisierung (1)
require(dplyr)
intercept_0 <- vorhersagen_df %>%
filter(SES == 0)
intercept_10 <- vorhersagen_df %>%
filter(SES == 10)
require(ggplot2)
require(ggrepel)
pd <- position_jitter(width = 0.5)
plot_reg <- ggplot(data = nlschools,
aes(x = SES, y = IQ, label = IQ)) +
geom_point(position = pd, alpha = 0.25) +
coord_cartesian(ylim = c(0, 20), xlim = c(0, 50)) +
theme_linedraw() +
theme(panel.grid = element_line(color = 'gray80'),
axis.text = element_text(size = 12),
axis.title = element_text(size = 12)) +
geom_smooth(method = 'lm') +
# geom_line(data = vorhersagen, color = 'red', size = 1.0) +
geom_point(data = intercept_0,
size = 3, shape = 8, color = 'red') +
geom_point(data = intercept_10,
size = 3, shape = 8, color = 'red') +
geom_text_repel(data = intercept_0,
box.padding = 0.5,
hjust = "left",
nudge_x = -10, nudge_y = -1) +
geom_text_repel(data = intercept_10,
box.padding = 0.5,
hjust = "left",
nudge_x = -5, nudge_y = 2); plot_regError in geom_text_repel(data = intercept_0, box.padding = 0.5, hjust = "left", : could not find function "geom_text_repel"Error in eval(expr, envir, enclos): object 'plot_reg' not foundVisualisierung (2)
require(ggplot2)
require(ggrepel)
pd <- position_jitter(width = 0.5)
plot_reg <- ggplot(data = nlschools,
aes(x = SES, y = IQ, label = IQ)) +
geom_point(position = pd, alpha = 0.25) +
coord_cartesian(ylim = c(0, 20), xlim = c(0, 50)) +
theme_linedraw() +
theme(panel.grid = element_line(color = 'gray80'),
axis.text = element_text(size = 12),
axis.title = element_text(size = 12)) +
geom_smooth(method = 'lm') +
geom_line(data = vorhersagen_df, color = 'red', linewidth = 1.0) +
geom_point(data = intercept_0, size = 3, shape = 8, color = 'red') +
geom_point(data = intercept_10, size = 3, shape = 8, color = 'red') +
geom_text_repel(data = intercept_0,
box.padding = 0.5,
hjust = "left",
nudge_x = -10, nudge_y = -1) +
geom_text_repel(data = intercept_10,
box.padding = 0.5,
hjust = "left",
nudge_x = -5, nudge_y = 2); plot_regError in geom_text_repel(data = intercept_0, box.padding = 0.5, hjust = "left", : could not find function "geom_text_repel"Error in eval(expr, envir, enclos): object 'plot_reg' not foundInterpretation der Ergebnisse:
- je höher SES, desto höher die Performanz der Schüler:innen.
- Zusätzlich können wir der Effekt von SES auf die Perfromanz genau beschreiben:
- Wenn SES um eine Einheit steigt, steigt die Performanz um 0.06. Das sollte für alle Schüler:innen ungefähr so stimmen (wir haben keine Gruppen/Klassen berücksichtigt).
- Das Modell nimmt an, das der Effekt von SES auf die performance konstant (oder fix) ist. Das bedeutet, dass der geschätzte Effekt für alle Personen gleich ist (oder sein sollte) und nicht von Person zu Person variiert (oder sich nicht zwischen Personengruppen unterschiedet).
- Fix-effects sind die Effekte, von denen man ausgeht, dass in der Population vorliegen (stabil sind).
Berücksichtigung der Gruppenzugehörigkeit (1)
Lasst uns die Analyse wiederholen. Allerdings werden wir dabei berücksichtigen, dass die Daten der Schüler:innen aus drei verschiedenen Klassen stammen.
- In einem ersten Schritt filtern wir die Daten nach Klassen.
- Danach können wir eine einfache Regression für jede Klasse berechnen und die Ergebnisse aus diesen Regressionen vergleichen.
Betrachten wir die folgende Abbildung:
require(MASS)
require(dplyr)
require(ggplot2)
erste_drei <- nlschools %>%
filter(class %in% unique(nlschools$class)[1:3])
ggplot(data = erste_drei, aes(x = SES, y = IQ, color = class)) +
geom_point(size = 1.0, alpha = 1.0) +
geom_smooth(method = 'lm', alpha = 0.50) +
theme_linedraw() +
coord_cartesian(ylim = c(0, 20)) +
labs(y = 'Test Score') +
theme(axis.text = element_text(size = 12)) +
facet_wrap(~ class, ncol = 3)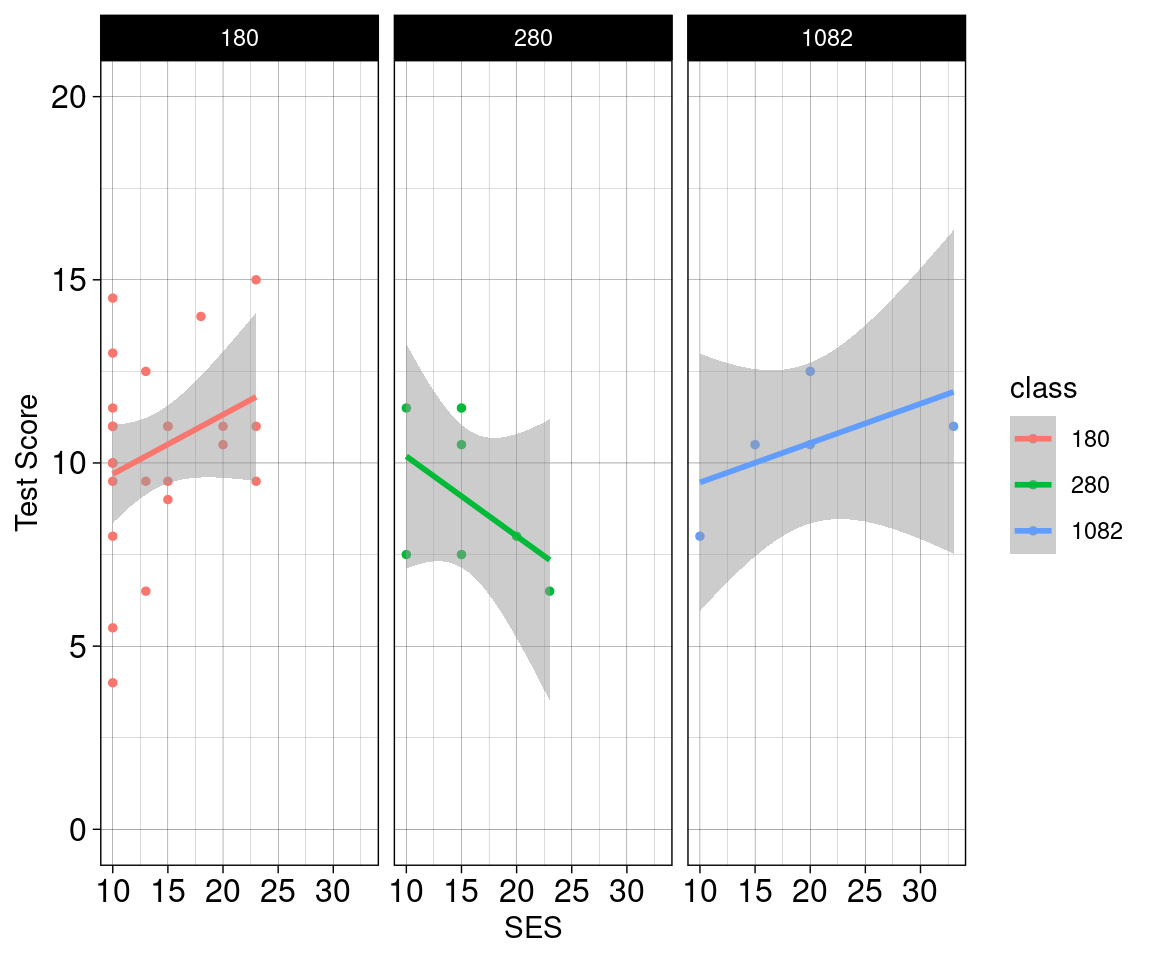
Berücksichtigung der Gruppenzugehörigkeit (2)
Aus unserer Analyse lässt sich nun ein \(\beta_{0}\) parameter und ein \(\beta_{1}\) parameter für jede gruppen Regression schätzen.
Nennen wir diese \(\beta_{0, j}\) und \(\beta_{1, j}\). Der index \(j\) bedeutet, dass jede klasse ihr eigenes \(\beta_{0}\) bzw. \(\beta_{1}\) hat.
Wir können diese auch “ausschrieben”:
- \(\widehat{\beta_{0, 1}}\) und \(\widehat{\beta_{1, 1}}\)für Gruppe 1.
- \(\widehat{\beta_{0, 2}}\) und \(\widehat{\beta_{1, 2}}\)für Gruppe 2.
- \(\widehat{\beta_{0, 3}}\) und \(\widehat{\beta_{1, 3}}\)für Gruppe 3.
Nun in R (Klasse 1):
klasse_1 <- nlschools %>%
filter(class %in% unique(nlschools$class)[1])
model_1 <- lm(data = klasse_1, IQ ~ SES)
summary(model_1)
Call:
lm(formula = IQ ~ SES, data = klasse_1)
Residuals:
Min 1Q Median 3Q Max
-5.6977 -1.0080 0.3023 1.3023 4.8023
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.0773 1.5809 5.109 3.56e-05 ***
SES 0.1620 0.1084 1.495 0.149
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.494 on 23 degrees of freedom
Multiple R-squared: 0.08857, Adjusted R-squared: 0.04894
F-statistic: 2.235 on 1 and 23 DF, p-value: 0.1485Nun in R (Klasse 2):
klasse_2 <- nlschools %>%
filter(class %in% unique(nlschools$class)[2])
model_2 <- lm(data = klasse_2, IQ ~ SES)
summary(model_2)
Call:
lm(formula = IQ ~ SES, data = klasse_2)
Residuals:
1 2 3 4 5 6 7
2.406639 1.406639 -0.004149 -1.593361 -2.682573 -0.850622 1.317427
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.3610 2.7335 4.522 0.00627 **
SES -0.2178 0.1703 -1.279 0.25693
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.998 on 5 degrees of freedom
Multiple R-squared: 0.2466, Adjusted R-squared: 0.09594
F-statistic: 1.637 on 1 and 5 DF, p-value: 0.2569Nun in R (Klasse 3):
klasse_3 <- nlschools %>%
filter(class %in% unique(nlschools$class)[3])
model_3 <- lm(data = klasse_3, IQ ~ SES)
summary(model_3)
Call:
lm(formula = IQ ~ SES, data = klasse_3)
Residuals:
1 2 3 4 5
0.49420 -0.04297 1.95703 -1.46862 -0.93963
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.39427 1.89266 4.435 0.0213 *
SES 0.10744 0.08994 1.194 0.3181
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.54 on 3 degrees of freedom
Multiple R-squared: 0.3223, Adjusted R-squared: 0.09641
F-statistic: 1.427 on 1 and 3 DF, p-value: 0.3181Zwischenfazit (1)
Bei der Betrachtung von und stellen wir fest, dass es deutliche Unterschiede zwischen den Klassen gibt hinsichtlich:
deren \(\beta_{0, j}\). Also deutliche Unterschiede in deren “Ausgangsleistungsniveaus”.
Woraun kann man dies erkennen?
- \(\beta_{0, j}\) ist der y-Achsenabschnitte, also die erwartete performance wenn SES = 0 ist.
den Zusammenhang zwischen SES und Perfromanz.
- dies lässt sich in unterschiedlichen \(\beta_{1, j}\) ablesen (die geschätzte Steigung der Modelle).
Zwischenfazit (2)
Die Zugehörigkeit zu einer Klasse verändert also den Effekt von SES (zumindest deskriptiv). In einer einfachen linearen Regression könnten wir dies nicht sehen, weil das Modell “naiv” gegenüber die Klassenzugehörigkeit der Personen ist.
Es is wahrschienlich am sinnvollsten den Effekt von ses und Klassenzugehörigkeit (Ein fixer between-subjects Faktor mit 3 Stufen: Klasse 1, Klasse 2, Klasse 3) in einem gemeinsammen Modell zu untersuchen:
Bei nur drei Klassen könnten wir Klassenzugehörigkeit als Kontrollvariable im Modell aufnehmen:
lm(data = erste_drei, IQ ~ class + SES)
Dies würde für die Abhängigkeiten, die auf die Klassenzugehörigkeit zurück gehen kontrollieren.
- Aber: Wenn wir keine Interaktion zwischen Klasse und ses zulassen, würde unser Modell nur für die Unterschiede der Klassen kontrollieren. Es würde also die Mittelwertsunterschiede der Klassen “heraus rechnen”.
Alternativ könnten wir Klassenzugehörigkeit als einen Moderator (Interaktion zwischen
classundSES) im Modell aufnehmen:- Dies würde uns erlauben die unterschiedliche \(\beta_{1, j}\) zu untersuchen.
Zwischenfazit (3)
Fixed-Effects Modelle sind Modelle in denen Prädiktoren aufgenommen werden um, deren Effekte auf einenm Kriterium zu unterscuchen.
Fixed-Effects sind also die Effekte von den Prädiktoren die uns interessieren.
Die Prädiktoren können in dem Modell aufgenommen werden, um dafür zu Kontrollieren, oder ihre “kombinierte” Effekte mit anderen Prädiktoen zu untersuchen.