MLM Seminar - Sitzung 3

Lineare Regression - Modellspezifikation und Modellparameter

Ziele

Am Ende des heutigen Termins sollten wir folgede Fragen beantworten können:

  • Wie unterschiedet sich eine einfache (lineare) Regression von einem Multi-Level Modell?
  • Mit welchen Werten (Modellparameter) kann man die Aussagen eines Modells untersuchen?
    • Welche Modellparameter gibt es?
    • Was sagen sie aus?
    • Wie interpretiert man die Modellparameter Intercept und Steigung.
  • Was versteht man unter “Fixed-Effects” und was sind “Fixed-Effects Modelle”?

Rückblick zur letzten Stunde

Konzequenzen hierarchisch organisierter Daten:

  • Beobachtungen innerhalb einer Gruppe (auch “Einheit”, oder “unit” genannt) ähneln sich stärker als die zwischen den Einheiten.
  • Dies verletzt die Unabhängigkeitsannahme der einfachen Regression
    • Viele Beobachtungen beeinflüssen sich gegenseitig oder werden in gleichermaßen beeinflüsst.
    • Die Beobachtungen sind also nicht von einander unabhängig.
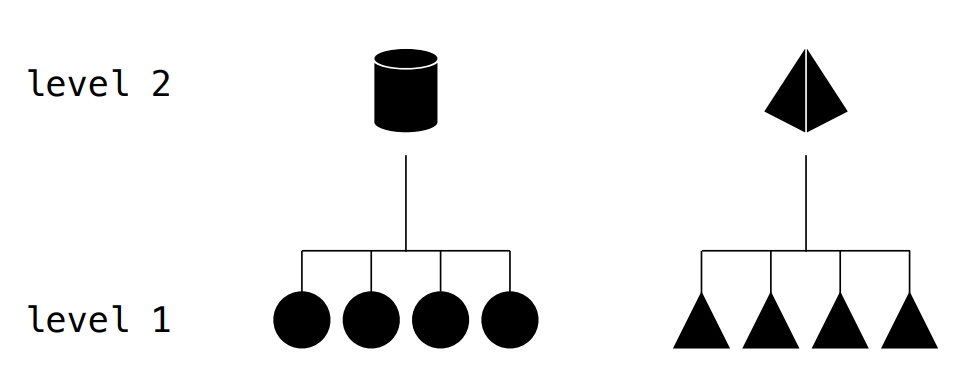
Multilevel data.

Die Grundidee eines Regressionsmodells

  • Die Ausprägung einer Variable hängt von der Ausprägung einer anderen Variable (oder Kombination von Variablen) ab.

  • Das Modell \(Y=f(x)+Error\):

    • Erklärt \(Y\) anhand von \(x\).
      • Wenn man \(x\) transformiert (i.e., \(f(x)\)) bekommt man einer Schätzung von \(Y\).

Beispiel 1

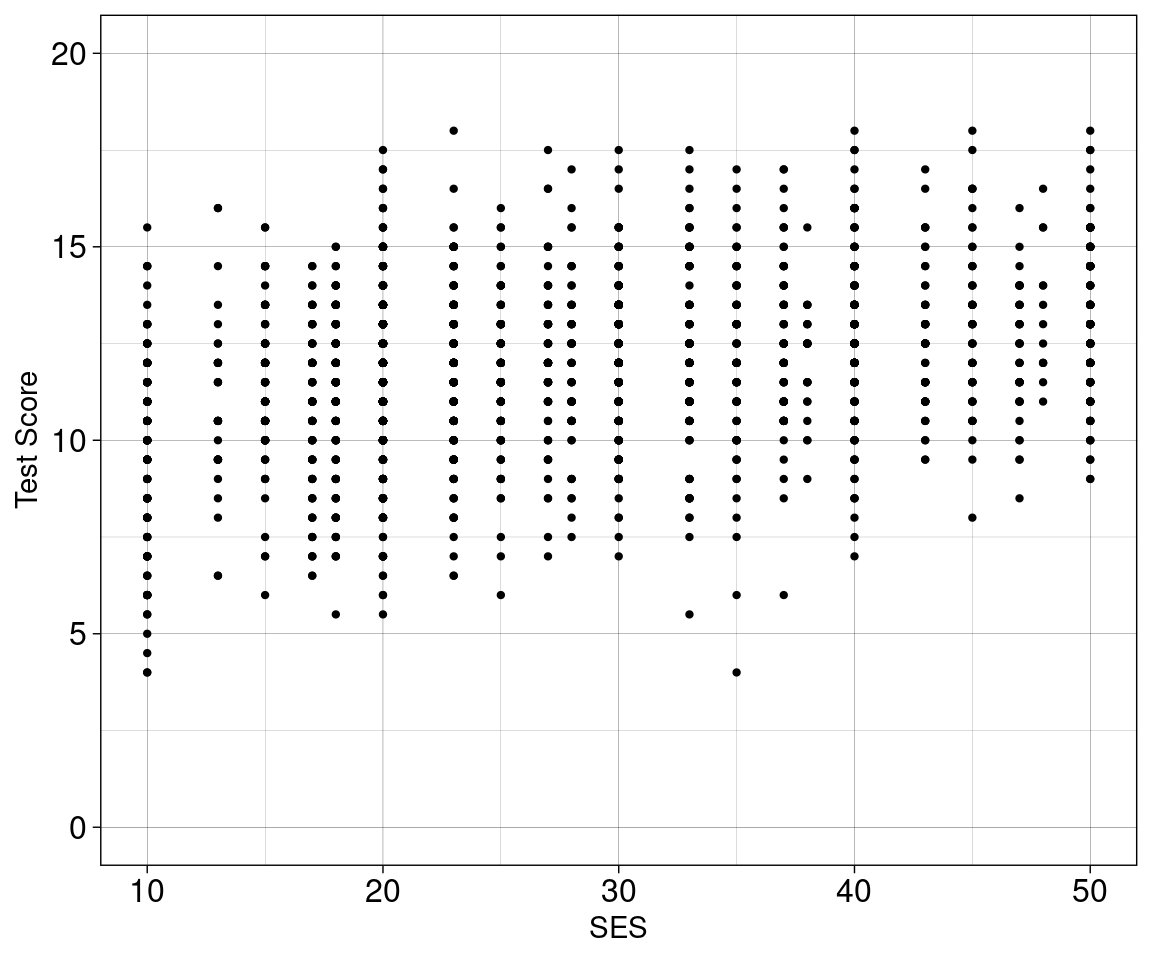
Beispiel 1 (linear model)

require(MASS)
require(ggplot2)

ggplot(data = nlschools, aes(x = SES, y = IQ)) +
    geom_point(ize = 0.8) +
    geom_smooth(method = 'lm') +
    theme_linedraw() +
    coord_cartesian(ylim = c(0, 20)) +
    labs(y = 'Test Score') +
    theme(axis.text = element_text(size = 12))

Die Fragestellung einer linearen Regression

Es soll untersucht werden, wie sich eine Variable \(X\) auf eine Variable \(Y\) auswirkt.

In unseren Beispiel:

  • Soziökonomischer Status (SES) von Schüler:innen (\(X\)) wirkt sich auf die Perfomanz (Test Score) der Schüler:innen in einem Test (\(Y\)).

  • Auf der \(Y\)-Achse sehen wir die Performanz.

    • Das ist die Variable, die vorhergesagt werden soll (auch Kriterium, oder Antwortvariable genannt).

  • Auf der \(X\)-Achse sehen wir die Prädiktor-Varible (das womit wir Performanz vorhersagen wollen).

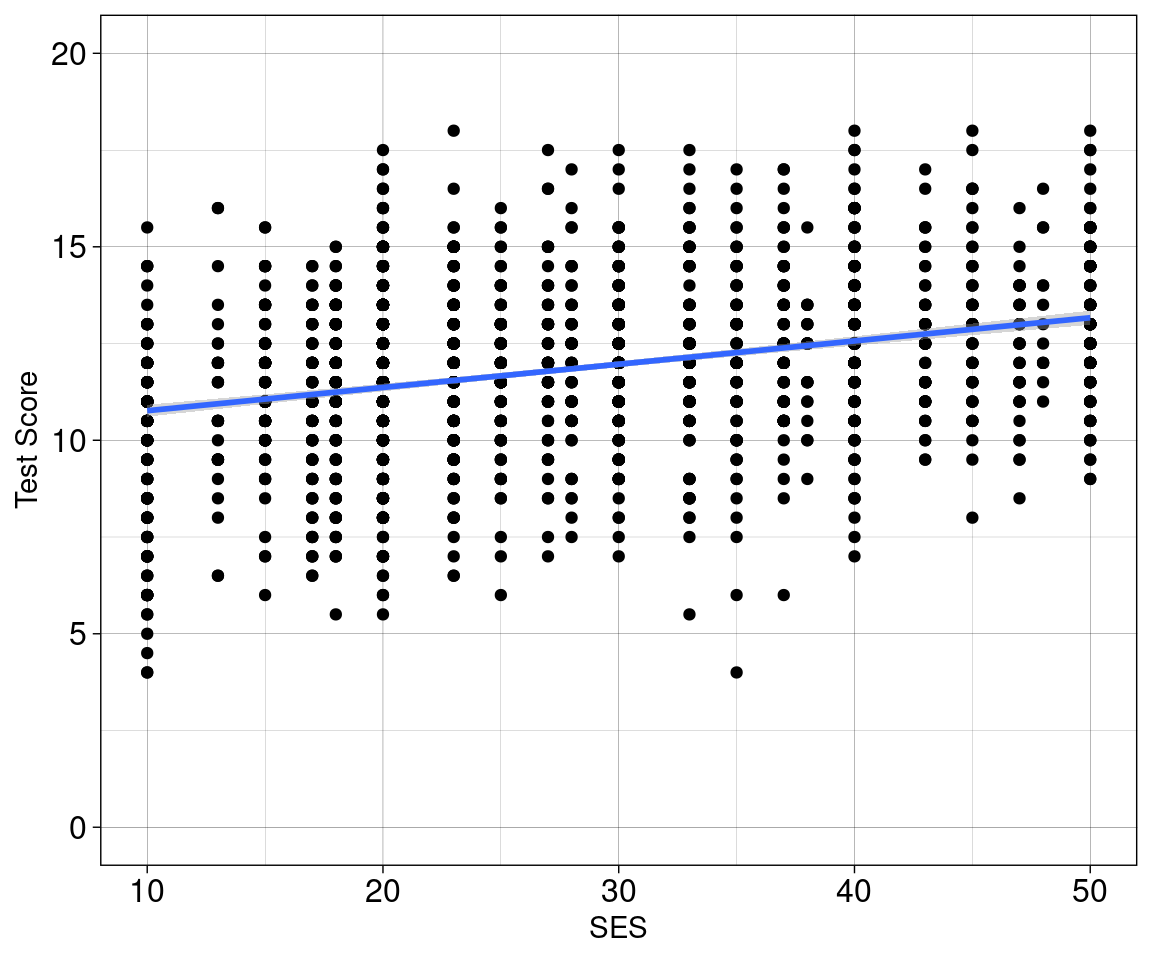
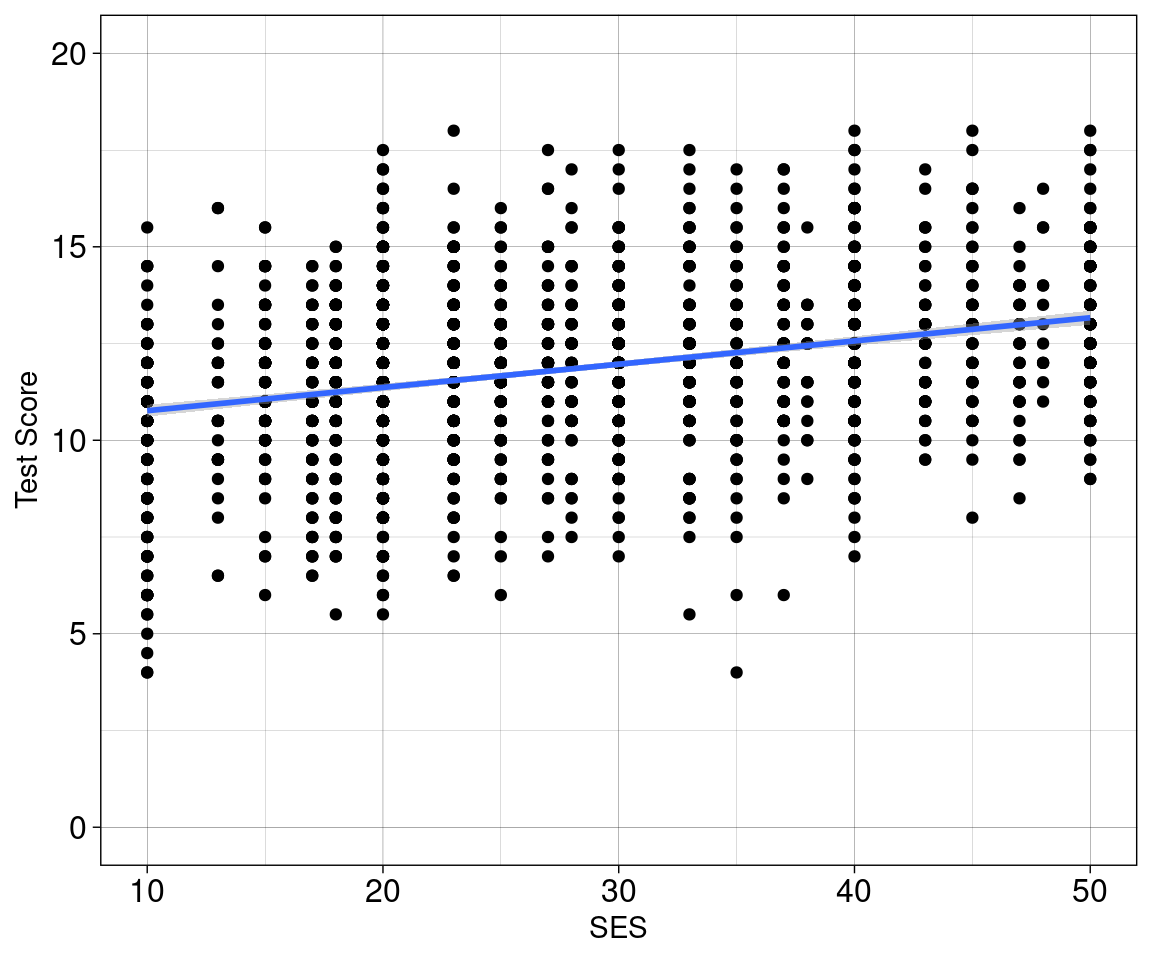
Modelparameter

\(\beta_{0}\)
Der Intercept des Modells (AKA - der y-Achsen-Abschnitt). \(\beta_{0}\) kann auch als: “Der Wert von \(Y\), wenn \(X\) = 0 ist”. - Oder, die Antwort auf die Frage: Welche Perfomanz zeigt eine Schüler:in, wenn sie ein Wert von 0 auf SES hat.

\(\beta_{1}\)
Der effekt vom Prädiktor \(X\) (AKA - Die Steigung der Regressionsgerade) \(\beta_{1}\) kann folgendermaßen vertanden werden: - Wenn SES um eine Einheit steigt (also von 0 zu 1), steigt die Performanz (im Mittel) um das \(\beta_{1}\)-fache.

require(MASS)
require(ggplot2)

model <- lm(data = nlschools, IQ ~ SES)
summary(model)

Call:
lm(formula = IQ ~ SES, data = nlschools)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.2659 -1.1651  0.0345  1.2147  6.4551 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 10.163000   0.112430   90.39   <2e-16 ***
SES          0.060084   0.003764   15.96   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.963 on 2285 degrees of freedom
Multiple R-squared:  0.1004,    Adjusted R-squared:  0.09996 
F-statistic: 254.9 on 1 and 2285 DF,  p-value: < 2.2e-16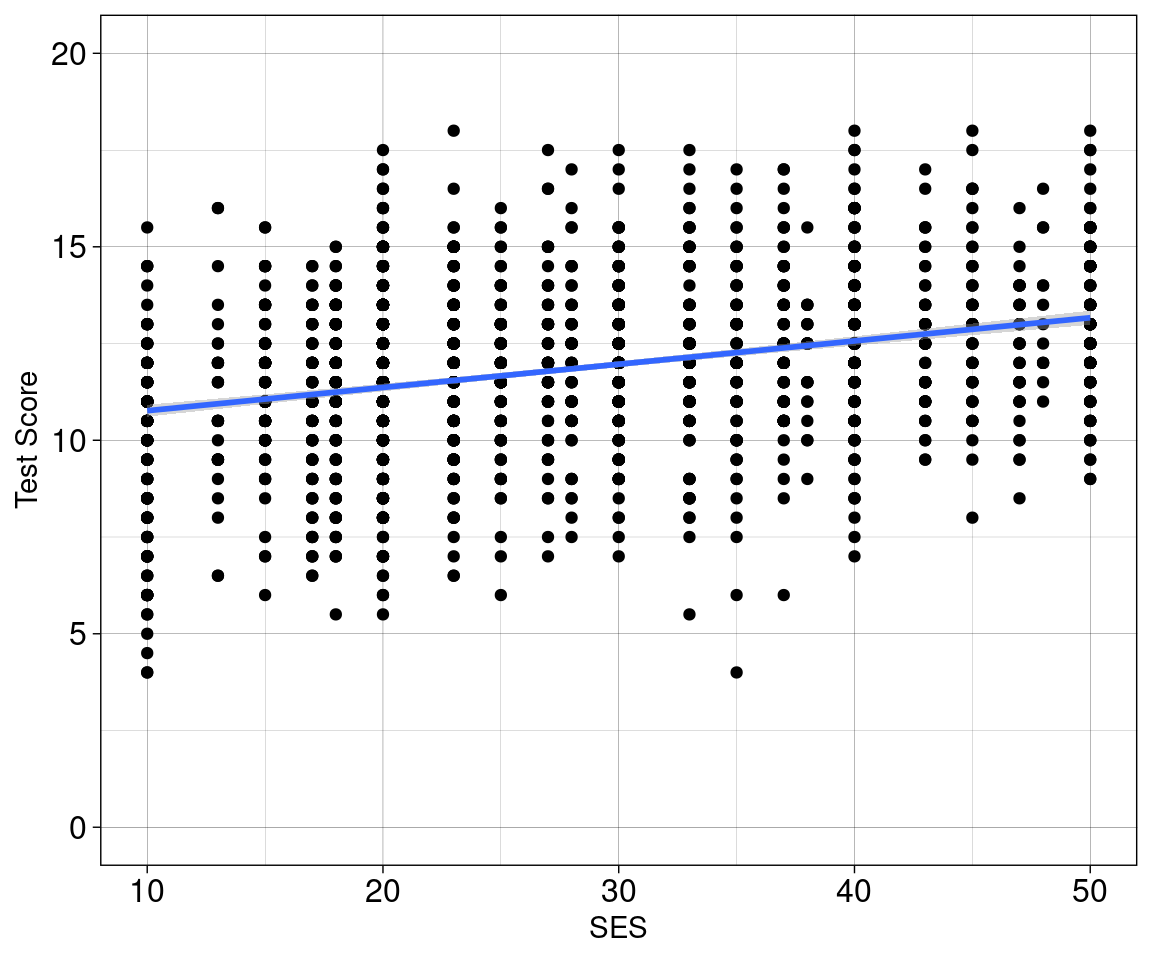

Modelvorhersahen

require(MASS)
require(ggplot2)

b0 = 10.163000
b1 = 0.060084
x = c(15, 25)

vorhersagen <- b0 + b1 * x
vorhersagen_df <- data.frame(SES = x, IQ = vorhersagen)

ggplot(data = nlschools, aes(x = SES, y = IQ)) +
    geom_point(size = 0.8, alpha = 0.5, color = 'gray') +
    geom_smooth(method = 'lm', alpha = 0.75) +
    geom_point(data = vorhersagen_df, size = 2.0, color = 'red', shape = 8) +
    theme_linedraw() +
    coord_cartesian(ylim = c(0, 20)) +
    labs(y = 'Test Score') +
    theme(axis.text = element_text(size = 12))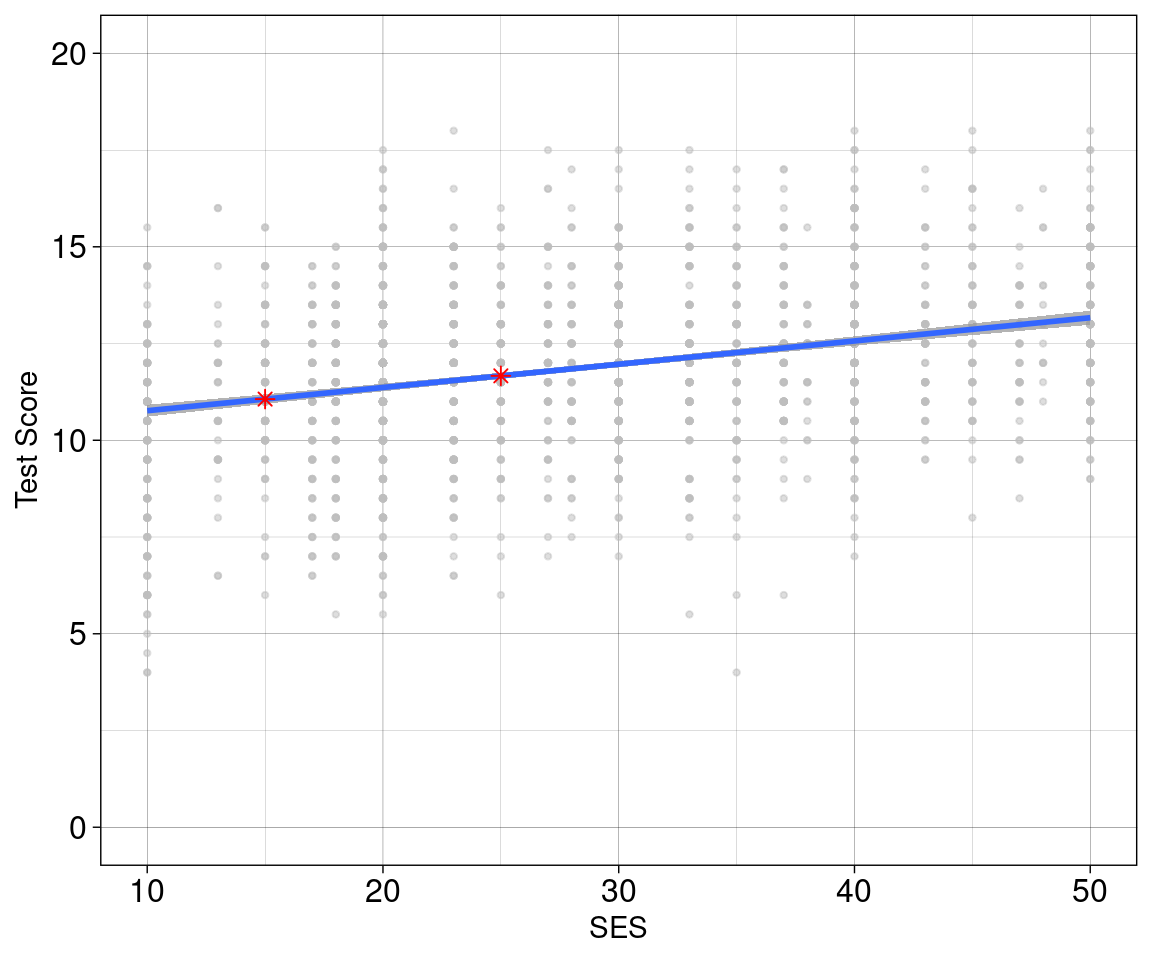

Zwischenfazit

Interpretation der Ergebnisse:

  • je höher SES, desto höher die Performanz der Schüler:innen.
  • Zusätzlich können wir der Effekt von SES auf die Perfromanz genau beschreiben:
    • Wenn SES um eine Einheit steigt, steigt die Performanz um 0.06. Das sollte für alle Schüler:innen ungefähr so stimmen (wir haben keine Gruppen/Klassen berücksichtigt).
  • Das Modell nimmt an, das der Effekt von SES auf die performance konstant (oder fix) ist. Das bedeutet, dass der geschätzte Effekt für alle Personen gleich ist (oder sein sollte) und nicht von Person zu Person variiert (oder sich nicht zwischen Personengruppen unterschiedet).
  • Fix-effects sind die Effekte, von denen man ausgeht, dass in der Population vorliegen (stabil sind).

Fortgeschrittene statistische Methoden II