Note
Click here to download the full example code
Plot beta coefficients from linear model estimation with sklearn¶
# Authors: Jose C. Garcia Alanis <alanis.jcg@gmail.com>
#
# License: BSD (3-clause)
import numpy as np
from sklearn.linear_model import LinearRegression
from mne.decoding import Vectorizer, get_coef
from mne.datasets import limo
from mne.stats import linear_regression
from mne.evoked import EvokedArray
Here, we’ll import only one subject and use the data to fit linear regression using LinearRegression from sklearn.linear_model. We’ll compare this results of the output of mne.stats.linear_regression
# subject id
subjects = [2]
# create a dictionary containing participants data
limo_epochs = {str(subj): limo.load_data(subject=subj) for subj in subjects}
# interpolate missing channels
for subject in limo_epochs.values():
subject.interpolate_bads(reset_bads=True)
# epochs to use for analysis
epochs = limo_epochs['2']
# only keep eeg channels
epochs = epochs.pick_types(eeg=True)
# save epochs information (needed for creating a homologous
# epochs object containing linear regression result)
epochs_info = epochs.info
tmin = epochs.tmin
Out:
1052 matching events found
No baseline correction applied
Adding metadata with 2 columns
0 projection items activated
0 bad epochs dropped
Computing interpolation matrix from 117 sensor positions
Interpolating 11 sensors
use epochs metadata to create design matrix for linear regression analyses
# add intercept
design = epochs.metadata.copy().assign(intercept=1)
# effect code contrast for categorical variable (i.e., condition a vs. b)
design['face a - face b'] = np.where(design['face'] == 'A', 1, -1)
# create design matrix with named predictors
predictors = ['intercept', 'face a - face b', 'phase-coherence']
design = design[predictors]
extract the data that will be used in the analyses
# get epochs data
data = epochs.get_data()
# number of epochs in data set
n_epochs = data.shape[0]
# number of channels and number of time points in each epoch
# we'll use this information later to bring the results of the
# the linear regression algorithm into an eeg-like format
# (i.e., channels x times points)
n_channels = data.shape[1]
n_times = len(epochs.times)
# vectorize (channel) data for linear regression
Y = Vectorizer().fit_transform(data)
fit linear model with sklearn
# here, we already have an intercept column in the design matrix,
# thus we'll call LinearRegression with fit_intercept=False
linear_model = LinearRegression(fit_intercept=False)
linear_model.fit(design, Y)
# next, we'll extract the resulting coefficients (i.e., betas)
# from the linear model estimator.
betas = get_coef(linear_model, 'coef_')
# notice that the resulting matrix of coefficients has a shape of
# number of observations in the vertorized channel data (i.e, these represent
# teh data points want to predict) by number of predictors.
print(betas.shape)
# thus, we can loop through the columns (i.e., the predictors) of the
# coefficient matrix and extract coefficients for each predictor and project
# them back to a channels x time points space.
lm_betas = dict()
for ind, predictor in enumerate(predictors):
# extract coefficients
beta = betas[:, ind]
# back projection to channels x time points
beta = beta.reshape((n_channels, n_times))
# create evoked object containing the back projected coefficients
# for each predictor
lm_betas[predictor] = EvokedArray(beta, epochs_info, tmin)
Out:
(25728, 3)
plot results of linear regression
# only show -250 to 500 ms
ts_args = dict(xlim=(-.25, 0.5))
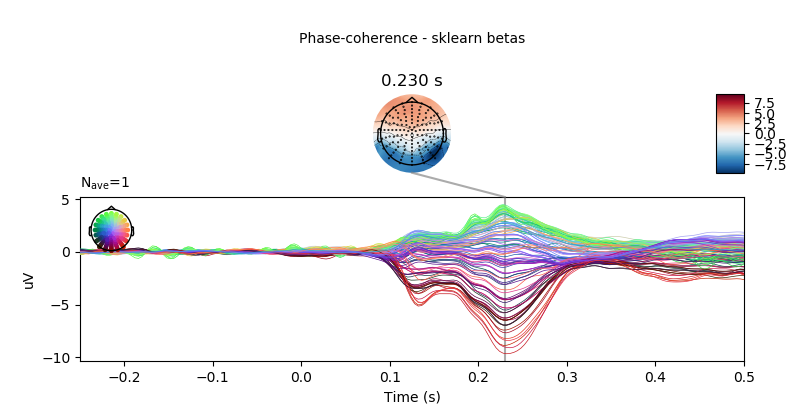
# visualise effect of phase-coherence for sklearn estimation method.
lm_betas['phase-coherence'].plot_joint(ts_args=ts_args,
title='Phase-coherence - sklearn betas',
times=[.23])
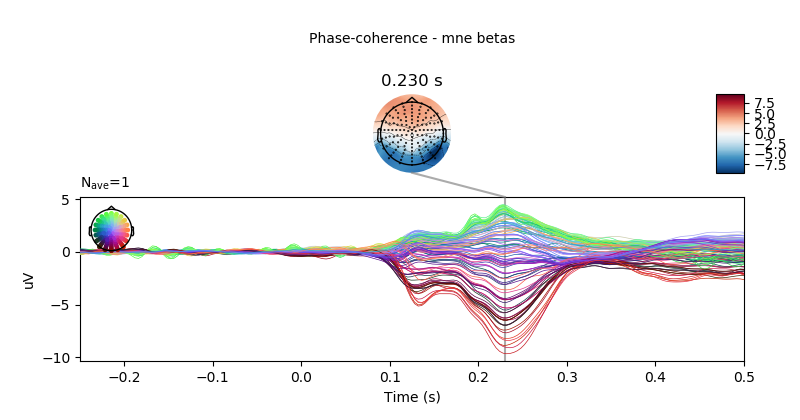
replicate analysis using mne.stats.linear_regression
reg = linear_regression(limo_epochs['2'], design, names=predictors)
# visualise effect of phase-coherence for mne.stats method.
reg['phase-coherence'].beta.plot_joint(ts_args=ts_args,
title='Phase-coherence - mne betas',
times=[.23])
Out:
Fitting linear model to epochs, (25728 targets, 3 regressors)
Done
Total running time of the script: ( 0 minutes 4.110 seconds)